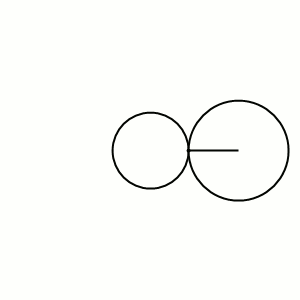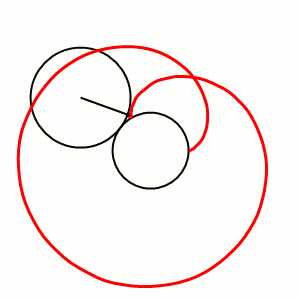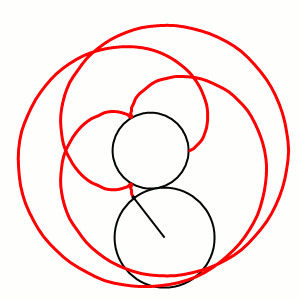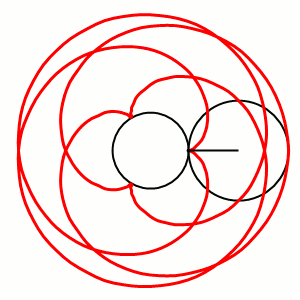The Irish Mathematical Trust
 rectified_icosahedral_honeycomb |  Formula Mathematics Equation Mathematical Symbol Geometry Information Concept |  MurlHoleSurfaceKnot-large |  EGMO2017IrishTeam |  honeycomb |
|---|
Mathematics and Art
Traditionally, people tend to see a divide between Maths and Art- it's thought that you can get involved in one or the other, but not both. This couldn't be further from the truth- the two have always enjoyed a symbiotic relationship, with mathematical concepts providing powerful techniques to all kinds of artists, and mathematicians seeing a fundamental beauty in the form of their work. Artistic flair and the scientific method drive each other through new innovations- maths forever invents new potential for a scenic view, while art lies at the heart of every 'Eureka!'-moment. Below are just a few examples of concepts in maths that link directly to art. For more, check out these websites: bugman123.com , mathforum.org/mathimages , rockini.name
Fractals
Fractal geometry is the study of "roughness"- Fractals are shapes that remain infinitely frayed, no matter how far you zoom in (technically, they're shapes with higher Hausdorff dimension than topological dimension). This gives them a very intricate appearance, which not only means they're good at modelling nature, but also that they look breathtaking.
Mandelbrot Set
The Mandelbrot Set of complex numbers is defined by the recurrence relation zn+1=zn²+z0 (the set contains all complex numbers z0 that don't cause the the orbit of zn to diverge). This is a close-up of the fractal boundary (one of the most famous fractals ever) of the set in the complex plane.
File:Mandel zoom 03 seehorse.jpg. Wolfgang Beyer.
License: https://creativecommons.org/licenses/by-sa/3.0/legalcode
Fractals in Nature
Approximations of Fractals can be found everywhere in the natural world, particularly in the growth of plants (plants like ferns, etc., often grow recursively, but can't achieve infinite complexity). This is the Romanesco Broccoli, whose top is self-similar- as you zoom in, you see scaled-down versions of the original broccoli. As well as this, its spirals are logarithmic and linked to the Fibonacci numbers.
Koch Snowflake
The Koch snowflake was one of the first fractals to be mathematically described and is defined in a simple recursive manner, starting with an equilateral triangle. At each step, its perimeter increases by a factor of 4/3, meaning the final snowflake has infinite perimeter. It also implies that the shape is log3(4) = 1.2619-dimensional!
Graphs of Parametric Equations
Mathematical Graphs in two and three dimensions can be extremely appealing to the eye, producing elegant curves and surfaces with potentially high complexity. Intricate shapes are most easily produced when co-ordinate variables are defined as functions of one or more parameters (like t, etc.). Here are a few examples of classes of parametric graphs, but it is impossible to even attempt to cover the whole field, and the concept can be generalised to higher dimensions.
Roulettes and Glissettes
A Roulette is the path traced out by a point on a curve as that curve slides along a second fixed curve. The concept sub-divides into a number of categories like cycloids and trochoids, each of which uses certain curves in certain ways. On the left is an epicycloid, where a small circle rolls around the circumference of a larger. A Glissette is the path of a point, or envelope of a curve, attached to another curve that slides along two other fixed objects.
By Dnttllthmmnm (Own work) [CC BY-SA 4.0 (http://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons
Lissajous Curves
The Lissajous Curves are the family of curves defined by the parametric equations x = Asin(at+δ), y = Bcos(bt). These curves can be extremely complex in appearance and are very beautiful (see the pictures on the left). They are sometimes used as the centrepieces of logos, as in the Australian Broadcasting Corporation (ABC) logo.
Parametric Surfaces
Parametric Surfaces are just the 3-D analogue of parametric curves: here, the x-, y- and z-coordinates of the surface are functions of two parameters. This can produce interesting results, like hyperbolic paraboloids, pseudospheres and cross-caps. To the left is the figure-8 immersion of the Klein bottle in 3-D.
Spidrons
Deformed Spidron
If a Spidron is cut out of paper and "bunched up" in the right way, a 3-D shape like the one on the left will result (it doesn't have to have a hexagonal outline- any regular polygon works). This can easily be done at home- click here for Spidron templates, or simply draw one yourself.
Spidron - folded paper, POV-Ray 3.6.1, 7/28/10, Paul Nylander
Dodeca-Spidroball - POV-Ray 3.6.1, 7/29/10
©Paul Nylander.
Spidronised Solids
"Spidronising" a polyhedron simply means putting a Spidron on each of its flat surfaces. Obviously, the shape of the Spidron must match the face to which it's being attached- the "Dodeca-Spidroball" on the left is based on a dodecahedron (12 pentagonal faces), and so each Spidron has five arms. Spidronised solids aren't of much practical use, but look really nice.
A Spidron® is a flat figure made of a number of triangles, where each triangle shares at least one side with another. They were first realised in 1979 by Dániel Erdély as homework in Ernő Rubik's design class. When cut out of paper, they can be deformed to make an intricate 3-D shape, which can in turn be attached to the face of a polyhedron to make a "spidronised" solid.
Sphidrons
A Sphidron is like a "smooth" Spidron.
7 Arm Sphidron - POV-Ray 3.6.1, 7/21/10, Paul Nylander
